Following every writer's advice on writing, which is to write often and about anything, I've been writing on my online scrapbook: from a short piece on sock strategy to a mid-sized piece on cargo pants to a large piece defending Apple to a series of pieces on digital content; that series spawned this post.
1. Digital content simplifies travel immensely
Comparing a packing list from 2000 to a packing list for 2012, I noticed that I now carry much less stuff and yet take much more content. But, in the post I originally wrote about this, I made the mistake of using the 2000 mindset to plan my 2012 content.
A single one-terabyte portable hard drive, smaller and lighter than one of the paperback scifi novels I carried in 2000, can take a vast library of music, podcasts, audiobooks, eBooks, television shows, and movies. I make sure that I take the content I want, then add as much as will fit.
Taking 200 eBooks, 100 audiobooks, 10 000 music tracks, and 300 videos, over one-hour each, for a four-week work trip might appear greedy -- especially since it's a work trip. But the point is that these represent options, not choices. While a choice is something you have to live with, an option is something you may use or not. And these are costless options, so no reason to not take them.
And, in keeping with the new social sharing meme: since there's a long stretch of travel involved, I'll be loading audiobooks for that in the iPod; if I were traveling tomorrow I'd listen to The Origins of Political Order from Pre-human Times to the French Revolution by Francis Fukuyama. I'd also load two Kindle books, as audiobooks aren't suited for airport noise: The Cemetery Of Prague by Umberto Eco and The Enchantress of Florence by Salman Rushdie. (Note: since I'm not traveling tomorrow, I availed myself of a dead tree copy of the latter book from the San Francisco Public Library; which brings up the next point.)
2. The economics of digital content create wealth for everyone
The free library one can build with iBooks, Kindle, and PDF from legal sources is comparable to some of the best libraries a wealthy person could own during the Gilded Age. Many technical books are also available as preprints from their authors.
There's a wealth of education and training opportunities available for free. For those who have no computers of their own, there are these buildings called "Public Library," which provide the computer and the internet access. This truly is an age of digital abundance.
So, when some technophobes start spouting nonsense like "the digital economy is broadening the chasm between the haves and the have-nots," all they're showing is their ignorance and a narrow focus on nominal dollars and who can buy the largest yacht or collectible $300 sneakers.
(This point is a special case of technological progress, which makes the lower middle class of 2012 much better off than those in the top 1% of income category in 1912 -- two words: modern dentistry, stealing from P J O'Rourke -- but the economics of digital content, namely negligible reproduction cost, make it an important special case.)
3. Changes to education due to digital content are overstated
Not to repeat myself over the problems of online education or the different components of education (prompted by the Kenan-Flagler Online MBA), but there are multiple components to education, only one and a half of which are covered by online materials.
First, there's the content side: learning how to program in R, for example. Motivated students can learn content from online sources; that's no surprise, since motivated students have always been able to learn from a precursor of online video textbooks (which is what lectures are): paper textbooks. And practice, of course, which may be tricky for some technical fields -- chemistry and nuclear physics come to mind -- but much less so for others. That's the one in "one and a half."
Second, there's certification of knowledge. Now that MIT decided that it would certify some courses for a small fee, that seems to be taken care of. But only in part (hence the "half"), since part of what the education system certifies in not purely content: getting to class (or at least labs) on time, performing consistently over long periods, in general doing things that one would rather not be doing. From a job market perspective, there's value in knowing whether a job candidate can do these things. Some people fret that education is more about fitting in than standing out, but for many jobs that's precisely what is desired of a new hire. This is part of the selection and screening made by education.
Third, there are skills beyond content that can only be obtained and observed in in-person interactions, like discussing and presenting, for example. Add to that the value of having a well-rounded foundation and, for technical fields, a problem-solving attitude. These are all things that can be observed in a few months on the job, but having an education institution do them first saves employers a lot of potential grief, especially if it's difficult to get rid of some people after you hire them (cf: Eurosclerosis).
Fourth, education institutions create networks of shared cultural values and experiences (observe the bonding between late middle age adolescents and late teenage adolescents at homecoming football games) and contacts, which are useful in later life. Networks on Facebook, Twitter, LinkedIn, Meetup, and Google Plus are useful for other purposes, but aren't complete replacements of a real social network. As in a network of people who have done things for each other.
Fifth, despite how much credentialism, nepotism, clique-ism, groupthink, and outright intellectual fraud can be laid at the foot of universities, for technical skills it's still the only really reliable source of information. The people who dedicate themselves to research in a technical field are forced to take multiple levels of abstraction into consideration (from the intro courses every researcher has to teach occasionally to the graduate seminars to the "where is this field going" moments of self-reflection) in their normal course of work. This perspective is uncommon in any other institution, and the only place where über-nerds of any field can be reliably found is the research institute or the university (where the nerds teach).
4. We still need to find a solution for the copyright problem
For all my love of open content and free software, and my loathing of the ridiculous means by which content providers hamper their own content and value proposition to get minor revenue enhancements, I have no illusions that content quality will be maintained without some protection of creators' rights.
Yes, anyone can write a book for a handful of dollars and some videos of cats playing piano have millions of views. But art photos that require travel or models, professionally recorded music (say the Berliner Philarmoniker doing a Beethoven symphony series), movies and television shows with good production values and actors, all of these cost a lot of money to make. And professional writers need to be paid -- some of them don't want to rely on public speaking or other non-writing forms of revenue. They want to write for a living. Some free content may be very good, but that mostly is paid for in some other way -- like the aforementioned free preprints of technical books. In general, good stuff means expensive to create, despite how cheap it may be to reproduce.
I for one don't want future Hawaii Five-O seasons to be fan-fic, amateur-made video snippets with Comicon rejects playing Grace Park's role.
So, I'm fine with buying the DVDs, especially since I like to listen to the commentary tracks; I find it ridiculous that ripping them with Handbrake would be a violation of the DMCA, even if I did so just to watch movies I own on my iPad. (Many DVDs now come bundled with a digital copy to appease people like me who are -- mostly -- on the side of content creators but find the revenue model intromissions in the consumption almost worthy of a switch to the content pirates side.)
A bonus point: I trust the cloud, but only as a last-resort back-up.
My work content is divided into three priority levels: Crucial, Important, and the rest. All work content is on the laptop hard drive, backed up on the portable hard drive. (All the entertainment content mentioned in point 1 is on the portable hard drive too, with the content I think I really want to consume during the trip on the laptop, the iPad, and the iPod Touch as well. Obviously these aren't the only copies I have of that content.)
Important content, about 11GB of class materials, is also backed up on four 16GB flash drives: two in my pockets, one on the laptop bag, and one in the rolling carry-on.
Crucial content, about 1GB of class materials (handouts, notes, essential images) and 500MB of research-in-progress (papers, notes, computations, code, experimental data) also goes on those 16GB flash drives plus two older 2GB drives and is backed up on DropBox and Amazon Cloud Drive.
Someone told me the 3-2-1 theory of backups: three copies, two formats, one off-site. I think the Many-Many-Many approach is better. And the cloud, that's all fine and dandy, but I want a local copy. For luck, say.
Non-work posts by Jose Camoes Silva; repurposed in May 2019 as a blog mostly about innumeracy and related matters, though not exclusively.
Saturday, January 28, 2012
Thursday, January 19, 2012
A tale of two long tails
Power law (Zipf) long tails versus exponential (Poisson) long tails: mathematical musings with important real-world implications.
There's a lot of talk about long tails, both in finance (where fat tails, a/k/a kurtosis, turn hedging strategies into a false sense of safety) and in retail (where some people think they just invented niche marketing). I leave finance for people with better salaries brainpower, and focus only on retail for my examples.
A lot of money can be made serving the customers on the long tail; that much we already knew from decades of niche marketing. The question is how much, and for this there are quite a few considerations; I will focus on the difference between exponential decay (Poisson) long tails and hyperbolic decay (power law) long tails and how that difference would impact different emphasis on long tail targeting (that is, how much to invest going after these niche customers), say for a bookstore.
A lot of money can be made serving the customers on the long tail; that much we already knew from decades of niche marketing. The question is how much, and for this there are quite a few considerations; I will focus on the difference between exponential decay (Poisson) long tails and hyperbolic decay (power law) long tails and how that difference would impact different emphasis on long tail targeting (that is, how much to invest going after these niche customers), say for a bookstore.
A Poisson distribution over $N\ge 0$ with parameter $\lambda$ has pdf:
$ \Pr(N=n|\lambda) =\frac{\lambda^{n}\, e^{-\lambda}}{n!}$.
A discrete power law (Zipf) distribution for $N\ge 1$ with parameter $s$ is given by:
$ \Pr(N=n|s) =\frac{n^{-s}}{\zeta(s)},$
where $\zeta(s)$ is the Riemann zeta function; note that it's only a scaling factor given $s$.
A couple of observations:
1. Because the power law has $\Pr(N=0|s)=0$, I'll actually use a Poisson + 1 process for the exponential long tail. This essentially means that the analysis would be restricted to people who buy at least one book. This assumption is not as bad as it might seem: (a) for brick-and-mortar retailers, this data is only collected when there's an actual purchase; (b) the process of buying a book at all -- which includes going to the store -- may be different from the process of deciding whether to buy a given book or the number of books to buy.
2. Since I'm not calibrating the parameters of these distributions on client data (which is confidential), I'm going to set these parameters to equalize the means of the two long tails. There are other approaches, for example setting them to minimize a measure of distance, say the Kullback-Leibler divergence or the mean square error, but the equal means is simpler.
The following diagram compares a Zipf distribution with $s=3$ (which makes $\mu=1.37$) and a 1 + Poisson process with $\lambda=0.37$ (click for larger):
The important data is the grey line, which maps into the right-side logarithmic scale: for all the visually impressive differences in the small numbers $N$ on the left, the really large ratios happen in the long tail. This is one of the issues a lot of probabilists point out to practitioners: it's really important to understand the behavior at the small probability areas of the distribution support, especially if they represent -- say -- the possibility of catastrophic losses in finance or the potential for the customers who buy large numbers of books.
An aside, from Seth Godin, about the importance of the heavy user segment in bookstores:
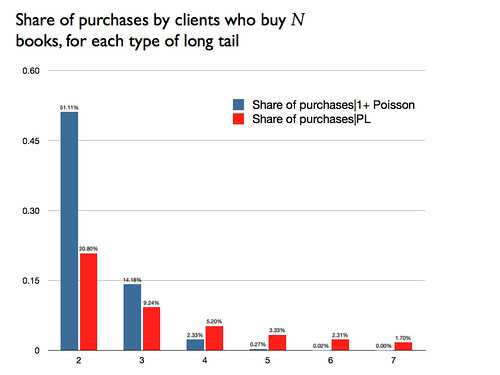
To illustrate the importance of even the relatively small ratios for a few books, this diagram shows the percentage of purchases categorized by size of purchase:
Yes, the large number of customers who buy a small number of books still gets a large percent of the total, but each of these is not a good customer to have: elaborating on Seth's post, these one-book customers are costly to serve, typically will buy a heavily-discounted best-seller and are unlikely to buy the high-margin specialized books, and tend to be followers, not influencers of what other customers will spend money on (so there are no spillovers from their purchase).
The small probabilities have been ignored long enough; finance is now becoming weary of kurtosis, marketing should go back to its roots and merge niche marketing with big data, instead of trying to reinvent the well-know wheel.
Lunchtime addendum: The differences between the exponential and the power law long tail are reproduced, to a smaller extent, across different power law regimes:
Note that the logarithmic scale implies that the increasing vertical distances with $N$ are in fact increasing probability ratios.
- - - - - - - - -
Well, that plan to make this blog more popular really panned out, didn't it? :-)
A couple of observations:
1. Because the power law has $\Pr(N=0|s)=0$, I'll actually use a Poisson + 1 process for the exponential long tail. This essentially means that the analysis would be restricted to people who buy at least one book. This assumption is not as bad as it might seem: (a) for brick-and-mortar retailers, this data is only collected when there's an actual purchase; (b) the process of buying a book at all -- which includes going to the store -- may be different from the process of deciding whether to buy a given book or the number of books to buy.
2. Since I'm not calibrating the parameters of these distributions on client data (which is confidential), I'm going to set these parameters to equalize the means of the two long tails. There are other approaches, for example setting them to minimize a measure of distance, say the Kullback-Leibler divergence or the mean square error, but the equal means is simpler.
The following diagram compares a Zipf distribution with $s=3$ (which makes $\mu=1.37$) and a 1 + Poisson process with $\lambda=0.37$ (click for larger):
The important data is the grey line, which maps into the right-side logarithmic scale: for all the visually impressive differences in the small numbers $N$ on the left, the really large ratios happen in the long tail. This is one of the issues a lot of probabilists point out to practitioners: it's really important to understand the behavior at the small probability areas of the distribution support, especially if they represent -- say -- the possibility of catastrophic losses in finance or the potential for the customers who buy large numbers of books.
An aside, from Seth Godin, about the importance of the heavy user segment in bookstores:
Amazon and the Kindle have killed the bookstore. Why? Because people who buy 100 or 300 books a year are gone forever. The typical American buys just one book a year for pleasure. Those people are meaningless to a bookstore. It's the heavy users that matter, and now officially, as 2009 ends, they have abandoned the bookstore. It's over.
To illustrate the importance of even the relatively small ratios for a few books, this diagram shows the percentage of purchases categorized by size of purchase:
Yes, the large number of customers who buy a small number of books still gets a large percent of the total, but each of these is not a good customer to have: elaborating on Seth's post, these one-book customers are costly to serve, typically will buy a heavily-discounted best-seller and are unlikely to buy the high-margin specialized books, and tend to be followers, not influencers of what other customers will spend money on (so there are no spillovers from their purchase).
The small probabilities have been ignored long enough; finance is now becoming weary of kurtosis, marketing should go back to its roots and merge niche marketing with big data, instead of trying to reinvent the well-know wheel.
Lunchtime addendum: The differences between the exponential and the power law long tail are reproduced, to a smaller extent, across different power law regimes:
Note that the logarithmic scale implies that the increasing vertical distances with $N$ are in fact increasing probability ratios.
- - - - - - - - -
Well, that plan to make this blog more popular really panned out, didn't it? :-)
Labels:
analytics,
business,
marketing,
mathematics,
Probability
Subscribe to:
Comments (Atom)