There are just too many possibilities.
Let's say we have one dependent variable, $y$, and ten independent variables, $x_1,\ldots,x_{10}$. How many models can we build? For simplicity let's keep our formulation linear (in the usual sense of the word, that is linear in the coefficients; see footnote).
Inexcusably wrong answer: 11 models.
Wrong answer: 1024 models.
Right-ish answer: $1.8 \times 10^{308}$ models.
Right answer: an infinity of models.
Ok, 1024 is the number of models which include at most one instance of each variable and no interaction. Something like
$ y = \beta_0 + \beta_1 \, x_1 + \beta_3 \, x_3 + \beta_7 \, x_7$ ,
of which there are $2^{10}$ models. (Since the constant $\beta_0$ can be zero by calibration, we'll include it in all models -- otherwise we'd have to demean the $y$.)
Once we consider possible interactions among variables, like $x_1 x_7 x_8$ for example, a three-way interaction, there are $2^{10}$ variables and interactions and therefore $2^{2^{10}}= 1.8 \times 10^{308}$ possible models with all interactions. For comparison, the number of atoms in the known universe is estimated to be in the order of $10^{80}$.
Of course, each variable can enter the model in a variety of functional forms: $x_1^{2}$, $\log(x_7)$, $\sin(5 \, x_9)$ or $x_3^{-x_{2}/2}$, for example, making it an infinite number of possibilities. (And there can be interactions between these different functions of different variables, obviously.)
(Added on August 11th.) Using polynomial approximations for generalized functions, say to the fourth degree, the total number of interactions is now $5^{10}=9765625$, as any variable may enter an interaction in one of five orders (0 through 4), and the total number of models is $2^{5^{10}}$ or around $10^{3255000}$. (End of addition.)
So here's a combinatorial riddle for statisticians: how can you identify a model out of, let's be generous, $1.8 \times 10^{308}$ with data in the exa- or petabyte range? That's almost three hundred orders of magnitude too little, methinks.
The main point is that any non-trivial set of variables can be modeled in a vast number of ways, which means that a limited number of models presented for appreciation (or review) necessarily includes an inordinate amount of judgement from the model-builder.
It's unavoidable, but seldom acknowledged.
--------------
The "linear in coefficients" point is the following. Take the following formulation, which is clearly non-linear in the $x$:
$y = \beta_0 + \beta_1 \, x_1^{1/4} + \beta_2 \, x_1 \, x_7$
but can be made linear very easily by making two changes of variables: $ z_1 = x_1^{1/4}$ and $z_2 = x_1 \, x_7$.
In contrast, the model $y = \alpha \, \sin( \omega \, t )$ cannot be linearized in coefficients $\alpha$ and $\omega$.
Non-work posts by Jose Camoes Silva; repurposed in May 2019 as a blog mostly about innumeracy and related matters, though not exclusively.
Thursday, July 28, 2011
Sunday, July 24, 2011
Three thoughts on presentation advice
As someone who makes presentations for a living,* I regularly peruse several blogs and forums on presentations. Here are three thoughts on presentation advice, inspired by that perusal.
1. The problem with much presentation advice is that it's a meta exercise: a presentation about presentations. And it falls into what I like to call the Norman Critique of Tufte's Table Argument (NCoTTA). From Don Norman's essay "In Defense Of Powerpoint":
2. When an attendee of a short talk I recently gave asked me for quick advice on presentations I said: have a simple clear statement, in complete sentences, of what your presentation is supposed to achieve. He was flummoxed; I assume he wanted the secret sauce for my slides.
Here's a slide from that talk:
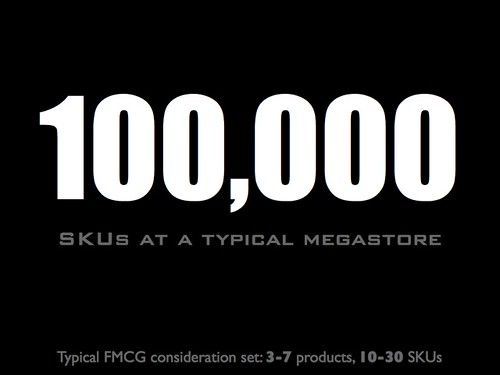
It's obvious that there is no secret sauce here; extending the cooking metaphor, what that slide shows is a good marinade: preparation. Though many presentation advice websites talk about rehearsal and working the room as preparation, what I mean is what this 3500-word post explains.
For example, knowing what the 100,000 SKU statistic is for, I chose to put the size of FMCG consideration sets as a footer, to contextualize the big number. Different uses of the big number get different footers to put it into the appropriate perspective. If all I wanted to do was illustrate how big that number is, I could say "if you bought a different SKU every day, you'd need almost 300 years to go through them all."
Most advice on presentations will not be useful because the content and the context of the presentation are much more important to the design of the presentation than generic rules. (Hence the NCoTTA problem so much advice has. Ditto for this slide, since I didn't explain what the talk was about.)
3. Speaking of Tufte, one of the things that separates him from the other presentation advocates is that he takes a full view of the communication process (partially illustrated in this post): from the speaker's data to the receiver's understanding. Here's a simple diagram to illustrate the sequence:
Most presentation advice is about the creation and, especially, the delivery of presentations. Tufte stands more or less alone as one who discusses the receiving and processing of presentation material: how to pay attention (not just being "engaged," but actually processing the information and checking for unstated assumptions, logical fallacies, psychological biases, or innumeracy) and how to elaborate on one's own, given presentation materials.
Other than Tufte and his constant reminder that receiving a presentation is an active process rather than a passive event, presentation coaches focus almost all their attention on the presenter-side processes. Many "Tufte followers" also miss this point: when processing a presentation by someone else they focus on the presentation itself (the slides, the design, the handouts) instead of the content of the presentation, i.e. the insights.
-- -- -- --
* Among other things, like teaching, creating original research, and writing.
1. The problem with much presentation advice is that it's a meta exercise: a presentation about presentations. And it falls into what I like to call the Norman Critique of Tufte's Table Argument (NCoTTA). From Don Norman's essay "In Defense Of Powerpoint":
Tufte doesn't overload the audience in his own talks—but that is because he doesn't present data as data, he presents data as examples of what slides and graphical displays might look like, so the fact that the audience might not have time to assimilate all the information is irrelevant.It's funny that Tufte is actually one of the people who least deserve the NCoTTA; most presentation coaches make that error more often and to greater depths.
2. When an attendee of a short talk I recently gave asked me for quick advice on presentations I said: have a simple clear statement, in complete sentences, of what your presentation is supposed to achieve. He was flummoxed; I assume he wanted the secret sauce for my slides.
Here's a slide from that talk:
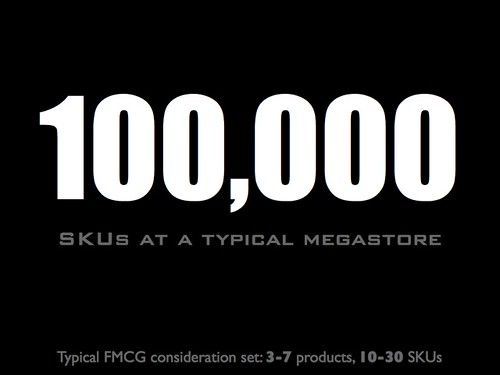
It's obvious that there is no secret sauce here; extending the cooking metaphor, what that slide shows is a good marinade: preparation. Though many presentation advice websites talk about rehearsal and working the room as preparation, what I mean is what this 3500-word post explains.
For example, knowing what the 100,000 SKU statistic is for, I chose to put the size of FMCG consideration sets as a footer, to contextualize the big number. Different uses of the big number get different footers to put it into the appropriate perspective. If all I wanted to do was illustrate how big that number is, I could say "if you bought a different SKU every day, you'd need almost 300 years to go through them all."
Most advice on presentations will not be useful because the content and the context of the presentation are much more important to the design of the presentation than generic rules. (Hence the NCoTTA problem so much advice has. Ditto for this slide, since I didn't explain what the talk was about.)
3. Speaking of Tufte, one of the things that separates him from the other presentation advocates is that he takes a full view of the communication process (partially illustrated in this post): from the speaker's data to the receiver's understanding. Here's a simple diagram to illustrate the sequence:
Most presentation advice is about the creation and, especially, the delivery of presentations. Tufte stands more or less alone as one who discusses the receiving and processing of presentation material: how to pay attention (not just being "engaged," but actually processing the information and checking for unstated assumptions, logical fallacies, psychological biases, or innumeracy) and how to elaborate on one's own, given presentation materials.
Other than Tufte and his constant reminder that receiving a presentation is an active process rather than a passive event, presentation coaches focus almost all their attention on the presenter-side processes. Many "Tufte followers" also miss this point: when processing a presentation by someone else they focus on the presentation itself (the slides, the design, the handouts) instead of the content of the presentation, i.e. the insights.
-- -- -- --
* Among other things, like teaching, creating original research, and writing.
Labels:
presentations
Friday, July 15, 2011
Adaptation, the key to success - Tim Harford at TED
This TED talk, Tim Harford on the folly of assuming one can control complex systems, is worth watching:
I have blogged about the problems with understanding causality in complex systems (in my case a system that is deceptively simple to describe but has complex behavior) before. I have Tim Harford's book Adapt, but haven't finished it yet; I will blog book notes (especially now that the Kindle App allows for copy-paste).
Experimentation, evolution, adaptation: the secret to a successful complex system. As in Nature so in business (and possibly other management fields).
I have blogged about the problems with understanding causality in complex systems (in my case a system that is deceptively simple to describe but has complex behavior) before. I have Tim Harford's book Adapt, but haven't finished it yet; I will blog book notes (especially now that the Kindle App allows for copy-paste).
Experimentation, evolution, adaptation: the secret to a successful complex system. As in Nature so in business (and possibly other management fields).
Wednesday, July 6, 2011
Thoughts on the Kenan-Flagler $89,000 online MBA (and the MBA degree in general)
I saw the news this morning that the Kenan-Flagler Business School at the University of North Carolina—Chapel Hill is starting a new online MBA and charging the same as for its in-class MBA, $\$89,000$.
Online MBAs have so far been mostly consigned to the low end of the MBA spectrum; Kenan-Flagler is a serious school with serious quality, so this is a game-changer. Which raises the important question:
Can a online MBA be worth the same as a regular, in-class MBA?
Futurology is a field fraught with error, so let's do what smart managers do at the beginning of a category lifecycle: think carefully about the likely path of the value proposition and the revenue models. The revenue model here is tuition plus alumni donations, same as for a in-class MBA; let's analyze the four components of the value proposition:
1. Technical business material. Things like how to value a put option; how to measure consumer preferences; how to brief an advertising agency; how to organize a value chain; how to analyze the potential of a market. These technical materials are learned the same way every other technical material is (math, science, engineering): mostly by practice. Practice comes from preparing for in-class discussions or homework. So, this part of the MBA value proposition is easily transferred to a online (or even textbook-based) education.
We may like to think that students are learning the technical material in class – because we are so good at explaining it, of course – but the students only learn the material for real when they put it into practice. More often than not, when they are gearing up to solve problems or analyze cases they have to review their notes or read the textbook. All this can work in a self-guided study, be it from the textbook or from online materials. It all depends on how the motivation (aka the assessment) is executed.
2. Managerial skills. Things like leadership, decision-making on-the-fly, presentation, consensus-building, teamwork. These are essential parts of Participant-Centered Learning, and very hard to do online. There's a point in a manager's training where she has to stop analyzing, raise her hand and – in front of a group of people who are trying to find fault with it – present her view of the case. The ability to convince others and get them to execute your decisions is fundamental to the job of manager and this type of experience does require the presence in a classroom.
In fact many critics of the MBA degree as preparation for management jobs state that the in-class experience is not enough to develop these skills and should be complemented with specific soft-skill development exercises, which – needless to say – have to be done in-class.
This might sound trivial, but many students have told me that, before doing it, they had no idea what it felt like to be called upon to defend a decision that they were 51.5% sure of and make it sound convincing (otherwise it would be dead on arrival). These are the kind of skills that make the difference between a back-office analyst and a line manager.
3. Networking and the broader community. Some non-MBAs, who tend to believe in conspiracies to explain their personal shortcomings, dismiss the MBA degree as just a network-building exercise. That is incorrect, but the network one creates as part of one's MBA is a valuable part of the program. A consultant might look good "on paper," but you save your firm a lot of grief (and money) because your old Strategy teammate told you that the guy can't tell a experience effect from a sound effect. This kind of networking will only develop with continued physical proximity.
But the community doesn't end there: there are the other cohorts (older and younger) and even the contacts with faculty (which in a business school may be more useful than, say, in a humanities school). There's also the broader campus community; some MBA students at a school that shall remain nameless, located close to the Longfellow Bridge on Memorial Drive in Cambridge, MA, use their affiliation with the larger Institute to contact faculty in areas that they might find useful; engineering comes to mind. This broader community might be available to online students, especially in this age of email, instant messaging, and videoconferencing.
4. Screening and signaling. Getting accepted into the program, completing the coursework, and paying a high tuition on the expectation that future earnings will more than make up for it are all signals a student sends to the market. The more selective the school is with its incoming class, the more informative that signal is. Since the same criteria can be applied to online and in-class students, the signal should be the same. (Whether the market accepts that the criteria are the same, that's a different story.)
At first I was flabbergasted that K-F was going to charge the same for the online as for the in-class MBA, but now I think that's actually smart on two levels: one, by having the same price for both, K-F signals that both programs are in fact two variants of the same degree; two, by keeping it expensive, they feed the third component of the signal, that those enrolling expect to make a lot of money, which means work hard.
So, what is the verdict?
On one hand, there are a few serious impediments to delivering the full value proposition of an MBA through a online environment. On the other hand, some of those issues can be mitigated with short "in campus" events. And, some people point out, many MBA students never really get the "soft-skill" parts that would be missing from an online MBA; even at K-F. (Even at Halberd, come to think of it.)
The market will decide, but a-priori there's no reason why, at least for technical jobs in business (including most of the consulting and finance jobs that MBAs crave) this wouldn't be a useful program.
Online MBAs have so far been mostly consigned to the low end of the MBA spectrum; Kenan-Flagler is a serious school with serious quality, so this is a game-changer. Which raises the important question:
Can a online MBA be worth the same as a regular, in-class MBA?
Futurology is a field fraught with error, so let's do what smart managers do at the beginning of a category lifecycle: think carefully about the likely path of the value proposition and the revenue models. The revenue model here is tuition plus alumni donations, same as for a in-class MBA; let's analyze the four components of the value proposition:
1. Technical business material. Things like how to value a put option; how to measure consumer preferences; how to brief an advertising agency; how to organize a value chain; how to analyze the potential of a market. These technical materials are learned the same way every other technical material is (math, science, engineering): mostly by practice. Practice comes from preparing for in-class discussions or homework. So, this part of the MBA value proposition is easily transferred to a online (or even textbook-based) education.
We may like to think that students are learning the technical material in class – because we are so good at explaining it, of course – but the students only learn the material for real when they put it into practice. More often than not, when they are gearing up to solve problems or analyze cases they have to review their notes or read the textbook. All this can work in a self-guided study, be it from the textbook or from online materials. It all depends on how the motivation (aka the assessment) is executed.
2. Managerial skills. Things like leadership, decision-making on-the-fly, presentation, consensus-building, teamwork. These are essential parts of Participant-Centered Learning, and very hard to do online. There's a point in a manager's training where she has to stop analyzing, raise her hand and – in front of a group of people who are trying to find fault with it – present her view of the case. The ability to convince others and get them to execute your decisions is fundamental to the job of manager and this type of experience does require the presence in a classroom.
In fact many critics of the MBA degree as preparation for management jobs state that the in-class experience is not enough to develop these skills and should be complemented with specific soft-skill development exercises, which – needless to say – have to be done in-class.
This might sound trivial, but many students have told me that, before doing it, they had no idea what it felt like to be called upon to defend a decision that they were 51.5% sure of and make it sound convincing (otherwise it would be dead on arrival). These are the kind of skills that make the difference between a back-office analyst and a line manager.
3. Networking and the broader community. Some non-MBAs, who tend to believe in conspiracies to explain their personal shortcomings, dismiss the MBA degree as just a network-building exercise. That is incorrect, but the network one creates as part of one's MBA is a valuable part of the program. A consultant might look good "on paper," but you save your firm a lot of grief (and money) because your old Strategy teammate told you that the guy can't tell a experience effect from a sound effect. This kind of networking will only develop with continued physical proximity.
But the community doesn't end there: there are the other cohorts (older and younger) and even the contacts with faculty (which in a business school may be more useful than, say, in a humanities school). There's also the broader campus community; some MBA students at a school that shall remain nameless, located close to the Longfellow Bridge on Memorial Drive in Cambridge, MA, use their affiliation with the larger Institute to contact faculty in areas that they might find useful; engineering comes to mind. This broader community might be available to online students, especially in this age of email, instant messaging, and videoconferencing.
4. Screening and signaling. Getting accepted into the program, completing the coursework, and paying a high tuition on the expectation that future earnings will more than make up for it are all signals a student sends to the market. The more selective the school is with its incoming class, the more informative that signal is. Since the same criteria can be applied to online and in-class students, the signal should be the same. (Whether the market accepts that the criteria are the same, that's a different story.)
At first I was flabbergasted that K-F was going to charge the same for the online as for the in-class MBA, but now I think that's actually smart on two levels: one, by having the same price for both, K-F signals that both programs are in fact two variants of the same degree; two, by keeping it expensive, they feed the third component of the signal, that those enrolling expect to make a lot of money, which means work hard.
So, what is the verdict?
On one hand, there are a few serious impediments to delivering the full value proposition of an MBA through a online environment. On the other hand, some of those issues can be mitigated with short "in campus" events. And, some people point out, many MBA students never really get the "soft-skill" parts that would be missing from an online MBA; even at K-F. (Even at Halberd, come to think of it.)
The market will decide, but a-priori there's no reason why, at least for technical jobs in business (including most of the consulting and finance jobs that MBAs crave) this wouldn't be a useful program.
Labels:
business,
education,
management,
MBAs
Tuesday, July 5, 2011
An annoying mistake people make using game theory
There's a lot of confusion between actions and strategies, at least in the minds (and presentations and papers, sadly) of some analytical modelers.
In a game each agent $i$ has a set of actions $\mathcal{A}_i$. For example, in the prisoners' dilemma, the actions are {Defect,Cooperate}; in the matching pennies game they are {H,T}.
A strategy for player $i$, $\sigma_i$, can be a simple action, in the case of pure strategies. For example, the strategy for the prisoners' dilemma is to Defect always, a pure strategy. So in this very particular case, the observed action, say $A_i \in \mathcal{A}_i$ coincides with the strategy $\sigma_i$.
A strategy can be a distribution $\sigma_i(A_i) \in \Delta(\mathcal{A}_i)$ over actions $A_i \in \mathcal{A}_i$, which is the case with mixed strategies. The balanced matching pennies game has a unique Nash equilibrium where both players play H with 1/2 probability and T with 1/2 probability.
And this is where a lot of modelers get confused.
I've heard (and read, sadly) modelers say "we never see mixed strategies, so we are going to look at equilibria with pure strategies only." (Usually even this statement is wrong. What they are looking at are "equilibria" in which players are forced to play pure strategies, which is different. These are usually not equilibria at all: typically they have competitive best responses in mixed strategies that dominate the "equilibrium" one.)
Of course you don't see mixed strategies. You never see any strategy; all you can see are actions. What you see in pure strategies is an action that happens to coincide with the strategy. In the matching pennies game, any play is executed by drawing from the distribution an action; that is what you see, say H. There's still an underlying $\sigma_i(H) = \sigma_i(T)=1/2$, but it is not visible; it must be inferred from the structure of the game's payoffs.
And, of course, a strategy can be a distribution $\sigma_i(A_i|\mathcal{I}_i)$ over $\mathcal{A}_i$ that is a function of information set of player $i$ at the time of play, $\mathcal{I}_i$, which makes things even more complicated. And more error-prone.
Some times during my first game theory course I thought all the formalism was a bit pedantic. Then I met people who didn't learn game theory properly, and realized that the formalism is there for a reason.
It removes the confusion.
Labels:
Game Theory,
technical
Saturday, July 2, 2011
Putting some thought into presentations - backward induction approach
Thinking about presentations as a persuasion device led me to this short exercise in backward induction (click through for larger picture):
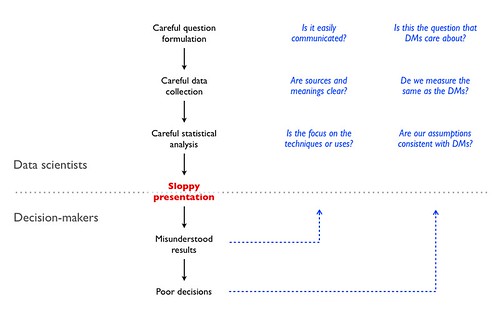
Sometimes a picture does capture more than one thousand words.

Sometimes a picture does capture more than one thousand words.
Labels:
presentations
Subscribe to:
Posts (Atom)
