Consider the following market share evolution model (which is a very bad model for many reasons, and not one that should be considered for any practical application):
(1) $s[t+1] = 4 s[t] (1-s[t])$
where $s[t]$ is the share at a given time period and $s[t+1]$ is the share in the next period. This is a very bad model for market share evolution, but I can make up a story to back it up, like so:
"When this product's market share increases, there are two forces at work: first, there's imitation (the $s[t]$ part) from those who want to fit it; second there's exclusivity (the $1-s[t]$ part) from those who want to be different from the crowd. Combining these into an equation and adding a scaling factor for shares to be in the 0-1 interval, we get equation (1)."
In younger days I used to tell this story as the set-up and only point out the model's problems after the entire exercise. In case you've missed my mention, this is a very bad model of market share evolution. (See below.)
Using the model in equation (1), and starting from a market share of 75%, we notice that this is an incredibly stable market:
(2) $s[t+1] = 4 \times 0.75 \times 0.25 = 0.75$.
Now, what happens if instead of a market share of 75%, we start with a market share of 75.00000001%? Yes, a $10^{-10}$ precision error. Then the market share evolution is that of this graph (click for bigger):
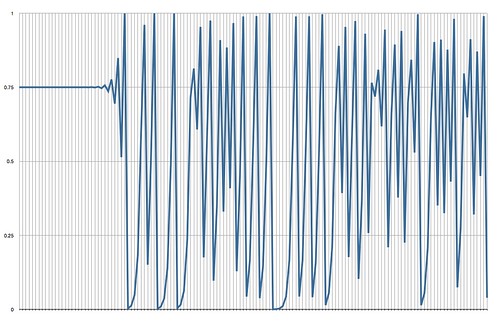
The point of this graph is not to show that the model is ridiculous, though it does get that point across quickly, but rather to set up the following question:
When did things start to go wrong?
When I run this exercise, about 95% of the students think the answer is somewhere around period 30 (when the big oscillations begin). Then I ask why and they point out the oscillations. But there is no change in the system at period 30; in fact, the system, once primed with $s[1]=0.7500000001$, runs without change.
The problem starts at period 1. Not 30. And the lesson, which about 5% of the class gets right without my having to explain it, is that the fact that a change becomes big and visible at time $T$ doesn't mean that the cause of that change is proximate and must have happened near $T$, say at $T-1$ or $T-2$.
In complex systems, very faraway causes may create perturbations long after people have forgotten the original cause. And as is for temporal cases, like this example, so it is for spatial cases.
A lesson many managers and pundits have yet to learn.
-- -- -- -- -- -- -- -- --
The most obvious reason why this is a bad model, from the viewpoint of a manager, is that it doesn't have managerial control variables, which means that if the model were to work, the value of that manager to the company would be nil. It also doesn't work empirically or make sense logically.