An old fight in a new battlefield: college tuition.
Apparently there's some talk of differentiated tuition for some degrees at the University of Nebraska in Lincoln. This gets people upset for all kinds of reasons. Let me summarize the two viewpoints underlying those reasons, using incredibly advanced tools from the core marketing class for non-business-major undergraduates, aka Marketing 101:
Viewpoint 1: Price Segmentation. Some degrees are more valuable than others to the people who get the degree; price can capture this difference in value as long as the university has some market power. Because people with STEM degrees (and some with economics and business degrees) will have on average higher lifetime earnings than those with humanities and "studies" degrees, there is a clear opportunity for this type of segmentation.
Viewpoint 2: Social Engineering. By making STEM and Econ/Business more expensive than other degrees, the UNL is incentivizing young people to go into these non-STEM degrees, wasting their time and money and creating a class of over-educated under-employable people. Universities should take into account the lifetime earnings implications of this incentive system and avoid its bad implications.
I have no problem with viewpoint 1 for a private institution, but I think that a public university like UNL should take viewpoint 2: lower the tuition for STEM and have very high tuition for the degrees with low lifetime earnings potential. (Yes, the opposite of what they're doing.)
It's a matter of social good: why waste students' time and money in these unproductive degrees? If a student has a lot of money, then by all means, let her indulge in the "college experience" for its own sake; if a student shows an outstanding ability for poetry, then she can get a scholarship or go into debt to pay the high humanities tuition. Everyone else: either learn something useful in college, get started in a craft in lieu of college (much better life than being a barista-with-college-degree), or enjoy some time off at no tuition cost.
I like art and think that our lives are enriched by the humanities (though not necessarily by what is currently studied in the Humanities Schools of universities, but that is a matter for another post). But there's a difference between something that one likes as a hobby (hiking, appreciating Japanese prints) and what one chooses as a job (decision sciences applied to marketing and strategy). My job happens to be something I'd do as a hobby, but most of my hobbies would not work as jobs.
Students who fail to identify what they are good at (their core strengths), what they do better than others (their differential advantages), and which activities will pay enough to support themselves (have high value potential) need guidance; and few messages are better understood than "this English degree is really expensive so make sure you think carefully before choosing it over a cheap one in Mechanical Engineering."
It's a rich society that can throw away its youth's time thusly.
Non-work posts by Jose Camoes Silva; repurposed in May 2019 as a blog mostly about innumeracy and related matters, though not exclusively.
Saturday, April 30, 2011
A situation in which I have to defend Gargle
I try not to judge, but ignorance and lax thinking of this magnitude is hard to ignore.
I'm far from being a Google fanboy and have in the past skewered a fanboy while reviewing his book; Google has plenty of people in public relations management, a lot of money to spend on it, and doesn't need my help; and every now and then I cringe when I hear people refer to Google's "don't be evil" slogan.
But this self-absorbed post makes me want to defend Google, for once. Here's the story as I see it, and as most people with even a passing interest in management and some minor real-world experience would probably see it:
A person was fired for indulging his personal politics at a contract site in a way that endangered the contract between his employer and the client (whose actions were legal and generous beyond the current norm).
I'll add that every company has a "class" system, using the scare quotes because the original poster chooses that word for emotional effect due to its association with reprehensible behavior (that doesn't apply here). The appropriate term is hierarchy.
Google apparently gives many fringe benefits to some contractors (red badge ones): free lunches, shuttles, access to internal talks; this is incredibly generous by common standards. But in the everyone should have everything everybody else does mindset of the original poster, the existence of different types of contractor (red vs yellow badges) is indicative of something bad.
Gee, how lucky Google was that this genius didn't learn about the discrimination in the use of the corporate jets. Imagine what his post would be like if he had learned that the interns couldn't use the company's 767 to take their friends to Bermuda.
He mentioned he was going to grad school; probably will fit in perfectly.
I'm far from being a Google fanboy and have in the past skewered a fanboy while reviewing his book; Google has plenty of people in public relations management, a lot of money to spend on it, and doesn't need my help; and every now and then I cringe when I hear people refer to Google's "don't be evil" slogan.
But this self-absorbed post makes me want to defend Google, for once. Here's the story as I see it, and as most people with even a passing interest in management and some minor real-world experience would probably see it:
A person was fired for indulging his personal politics at a contract site in a way that endangered the contract between his employer and the client (whose actions were legal and generous beyond the current norm).
I'll add that every company has a "class" system, using the scare quotes because the original poster chooses that word for emotional effect due to its association with reprehensible behavior (that doesn't apply here). The appropriate term is hierarchy.
Google apparently gives many fringe benefits to some contractors (red badge ones): free lunches, shuttles, access to internal talks; this is incredibly generous by common standards. But in the everyone should have everything everybody else does mindset of the original poster, the existence of different types of contractor (red vs yellow badges) is indicative of something bad.
Gee, how lucky Google was that this genius didn't learn about the discrimination in the use of the corporate jets. Imagine what his post would be like if he had learned that the interns couldn't use the company's 767 to take their friends to Bermuda.
He mentioned he was going to grad school; probably will fit in perfectly.
Labels:
google,
management
Saturday, April 23, 2011
The illusion of understanding cause and effect in complex systems
Also know as the "you're probably firing the wrong person" effect.
Consider the following market share evolution model (which is a very bad model for many reasons, and not one that should be considered for any practical application):
(1) $s[t+1] = 4 s[t] (1-s[t])$
where $s[t]$ is the share at a given time period and $s[t+1]$ is the share in the next period. This is a very bad model for market share evolution, but I can make up a story to back it up, like so:
"When this product's market share increases, there are two forces at work: first, there's imitation (the $s[t]$ part) from those who want to fit it; second there's exclusivity (the $1-s[t]$ part) from those who want to be different from the crowd. Combining these into an equation and adding a scaling factor for shares to be in the 0-1 interval, we get equation (1)."
In younger days I used to tell this story as the set-up and only point out the model's problems after the entire exercise. In case you've missed my mention, this is a very bad model of market share evolution. (See below.)
Using the model in equation (1), and starting from a market share of 75%, we notice that this is an incredibly stable market:
(2) $s[t+1] = 4 \times 0.75 \times 0.25 = 0.75$.
Now, what happens if instead of a market share of 75%, we start with a market share of 75.00000001%? Yes, a $10^{-10}$ precision error. Then the market share evolution is that of this graph (click for bigger):
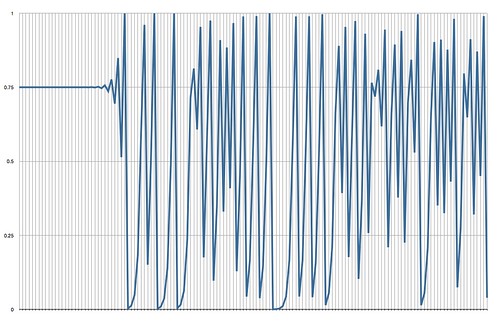
The point of this graph is not to show that the model is ridiculous, though it does get that point across quickly, but rather to set up the following question:
When did things start to go wrong?
When I run this exercise, about 95% of the students think the answer is somewhere around period 30 (when the big oscillations begin). Then I ask why and they point out the oscillations. But there is no change in the system at period 30; in fact, the system, once primed with $s[1]=0.7500000001$, runs without change.
The problem starts at period 1. Not 30. And the lesson, which about 5% of the class gets right without my having to explain it, is that the fact that a change becomes big and visible at time $T$ doesn't mean that the cause of that change is proximate and must have happened near $T$, say at $T-1$ or $T-2$.
In complex systems, very faraway causes may create perturbations long after people have forgotten the original cause. And as is for temporal cases, like this example, so it is for spatial cases.
A lesson many managers and pundits have yet to learn.
-- -- -- -- -- -- -- -- --
The most obvious reason why this is a bad model, from the viewpoint of a manager, is that it doesn't have managerial control variables, which means that if the model were to work, the value of that manager to the company would be nil. It also doesn't work empirically or make sense logically.
Consider the following market share evolution model (which is a very bad model for many reasons, and not one that should be considered for any practical application):
(1) $s[t+1] = 4 s[t] (1-s[t])$
where $s[t]$ is the share at a given time period and $s[t+1]$ is the share in the next period. This is a very bad model for market share evolution, but I can make up a story to back it up, like so:
"When this product's market share increases, there are two forces at work: first, there's imitation (the $s[t]$ part) from those who want to fit it; second there's exclusivity (the $1-s[t]$ part) from those who want to be different from the crowd. Combining these into an equation and adding a scaling factor for shares to be in the 0-1 interval, we get equation (1)."
In younger days I used to tell this story as the set-up and only point out the model's problems after the entire exercise. In case you've missed my mention, this is a very bad model of market share evolution. (See below.)
Using the model in equation (1), and starting from a market share of 75%, we notice that this is an incredibly stable market:
(2) $s[t+1] = 4 \times 0.75 \times 0.25 = 0.75$.
Now, what happens if instead of a market share of 75%, we start with a market share of 75.00000001%? Yes, a $10^{-10}$ precision error. Then the market share evolution is that of this graph (click for bigger):

The point of this graph is not to show that the model is ridiculous, though it does get that point across quickly, but rather to set up the following question:
When did things start to go wrong?
When I run this exercise, about 95% of the students think the answer is somewhere around period 30 (when the big oscillations begin). Then I ask why and they point out the oscillations. But there is no change in the system at period 30; in fact, the system, once primed with $s[1]=0.7500000001$, runs without change.
The problem starts at period 1. Not 30. And the lesson, which about 5% of the class gets right without my having to explain it, is that the fact that a change becomes big and visible at time $T$ doesn't mean that the cause of that change is proximate and must have happened near $T$, say at $T-1$ or $T-2$.
In complex systems, very faraway causes may create perturbations long after people have forgotten the original cause. And as is for temporal cases, like this example, so it is for spatial cases.
A lesson many managers and pundits have yet to learn.
-- -- -- -- -- -- -- -- --
The most obvious reason why this is a bad model, from the viewpoint of a manager, is that it doesn't have managerial control variables, which means that if the model were to work, the value of that manager to the company would be nil. It also doesn't work empirically or make sense logically.
Labels:
analytics,
change,
management,
marketing,
mathematics
Why asymmetric dominance demonstrates preference inconsistency and spoils market research tools
(Another old CB handout LaTeXed into the blog.)
Recall from the example of ``The Economist'' [in Dan Ariely's Predictably Irrational] that the options to choose from are
$A$: paper-only for 125
$B$: internet only for 65
$C$: paper + internet for 125
When presented with a choice set $\{B,C\}$ about half of the subjects pick $B$; when presented with choice set $\{A,B,C\}$ almost all subjects pick $C$. This presents a logic problem, since if C is better than B then there is no reason why it's not chosen when A is not present; if B is better than C, then there is no reason why C is chosen when A is present.
Logic is not our problem.
The reason we care about ``rational'' models is that they are the foundation of market research tools we like. In particular, we like one called utility. The idea is that we can assign numbers to choice options in a way that these numbers summarize choices (sounds like conjoint analysis, doesn't it?). Once we have these numbers we can decompose them along the dimensions of the options (yep, conjoint analysis!) and use the decomposition to determine trade-offs among products. We denote the number assigned to choice $X$ by $u(X)$.
As long as there is one number * that is assigned to each choice option by itself, we can use utility theory to analyze actual choices and determine what the drivers of customer decisions are. One number per option. Consumers facing a number of options pick that which has the highest number; this is called ``utility maximization,'' is extremely misunderstood by the general public, politicians, and the media, and all it means is that the customers choose the option they like the best, as captured by their consistent choices.
That is the problem.
Suppose we observe $B$ chosen from $\{B,C\}$; then utility theory says $u(B) > u(C)$. But then, if we observe $C$ picked from $\{A,B,C\}$ we have to conclude $u(C) > u(B)$. There are no numbers that can fit both cases at the same time, so there is no utility function. No utility function means no conjoint, no choice model, no market research --- unless we account for asymmetric dominance itself, which requires a lot of technical expertise. And forget about simple trade-off methods.
Meaning what?
Suppose we want to ignore the mathematical impossibility of coming up with a utility function (who cares about economics anyway?) and decide to measure the part-worths by hook or by crook. So we divide the products in their constituent parts, in this case $p$ for paper and $i$ for internet. The options become $\{(p,125), (i,65),(p+i,125)\}$. We can try to make a disaggregate estimation of the part-worths using a conjoint/tradeoff model.
The problem persists.
If $(i,65)$ is chosen over $(p+i,125)$, that means that the part-worth of $p$ is less than 60. That is the conclusion we can get from the choice of $B$ from $\{B,C\}$. If $(p+i,125)$ is chosen over $(i,65)$, that means that the part-worth of $p$ is more than 60. That is the conclusion we can get from the choice of $C$ from $\{A,B,C\}$.
A marketer using these two observations to design an offering cannot determine the part-worth of one of the components: the $p$ part. It's above 60 and under 60 at the same time.
Oops.
-- -- -- -- -- -- -- -- --
* Up to any increasing transformation of the utility function numbers, if you want to get technical; we don't, and it doesn't matter anyway.
Recall from the example of ``The Economist'' [in Dan Ariely's Predictably Irrational] that the options to choose from are
$A$: paper-only for 125
$B$: internet only for 65
$C$: paper + internet for 125
When presented with a choice set $\{B,C\}$ about half of the subjects pick $B$; when presented with choice set $\{A,B,C\}$ almost all subjects pick $C$. This presents a logic problem, since if C is better than B then there is no reason why it's not chosen when A is not present; if B is better than C, then there is no reason why C is chosen when A is present.
Logic is not our problem.
The reason we care about ``rational'' models is that they are the foundation of market research tools we like. In particular, we like one called utility. The idea is that we can assign numbers to choice options in a way that these numbers summarize choices (sounds like conjoint analysis, doesn't it?). Once we have these numbers we can decompose them along the dimensions of the options (yep, conjoint analysis!) and use the decomposition to determine trade-offs among products. We denote the number assigned to choice $X$ by $u(X)$.
As long as there is one number * that is assigned to each choice option by itself, we can use utility theory to analyze actual choices and determine what the drivers of customer decisions are. One number per option. Consumers facing a number of options pick that which has the highest number; this is called ``utility maximization,'' is extremely misunderstood by the general public, politicians, and the media, and all it means is that the customers choose the option they like the best, as captured by their consistent choices.
That is the problem.
Suppose we observe $B$ chosen from $\{B,C\}$; then utility theory says $u(B) > u(C)$. But then, if we observe $C$ picked from $\{A,B,C\}$ we have to conclude $u(C) > u(B)$. There are no numbers that can fit both cases at the same time, so there is no utility function. No utility function means no conjoint, no choice model, no market research --- unless we account for asymmetric dominance itself, which requires a lot of technical expertise. And forget about simple trade-off methods.
Meaning what?
Suppose we want to ignore the mathematical impossibility of coming up with a utility function (who cares about economics anyway?) and decide to measure the part-worths by hook or by crook. So we divide the products in their constituent parts, in this case $p$ for paper and $i$ for internet. The options become $\{(p,125), (i,65),(p+i,125)\}$. We can try to make a disaggregate estimation of the part-worths using a conjoint/tradeoff model.
The problem persists.
If $(i,65)$ is chosen over $(p+i,125)$, that means that the part-worth of $p$ is less than 60. That is the conclusion we can get from the choice of $B$ from $\{B,C\}$. If $(p+i,125)$ is chosen over $(i,65)$, that means that the part-worth of $p$ is more than 60. That is the conclusion we can get from the choice of $C$ from $\{A,B,C\}$.
A marketer using these two observations to design an offering cannot determine the part-worth of one of the components: the $p$ part. It's above 60 and under 60 at the same time.
Oops.
-- -- -- -- -- -- -- -- --
* Up to any increasing transformation of the utility function numbers, if you want to get technical; we don't, and it doesn't matter anyway.
Labels:
analytics,
consumer behavior,
marketing
Subscribe to:
Comments (Atom)