Tracking consumption was simple: I have two french presses, both used for tea; the smaller one (1 liter) brews the caffeine equivalent of two espressos (80mg each, or 160 total) and the larger one (1.5 liter) brews the equivalent of three espressos (240mg). I just made a note of when I finished with one of the french presses and which it was.
To convert consumption into blood level, we need a state equation. We make the following assumptions:
- Caffeine level on wakeup is zero (an approximation).
- Time $t$ is discrete and measured in half-hours.
- Caffeine half-life in the body is two hours.*
$\qquad L(t) = c(t) + 0.8409 \times L(t-1)$
where $L(t)$ is the level and $c(t)$ is the consumption at time $t$. This equation is an exponential decay process with a half-life of two hours: for a given $t=T$, assuming no consumption,
$\qquad L(T+4) = (0.8409)^4 \times L(T) = 0.5000 \times L(T)$.
(Two hours is 4 half-hours, since we're using the half-hour as the time unit.)
Putting the consumption and the initial condition into the equation and graphing it on a scale for the day in question we get
-- -- -- --
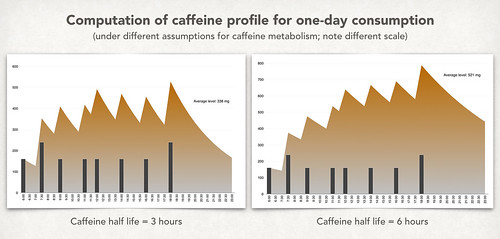
* I got this number from a doctor, but several sources have told me it's too low. Online sources point to a half-life of 3-6 hours. This changes the coefficient for $L(t-1)$ in the equation above to somewhere between 0.8909 (for three hours) to 0.9439 (for six hours). Possibly there's an update to this post in the future to deal with that.
Update in the future: I did the computations (click to embiggen):
