Essentially the number of edges is $N(N-1)/2$ so the number of possible topologies is two raised to the number of edges, capturing every possible case where an edge can either be present or absent. For a directed network the number of edges is twice that of those in an undirected network so the number of possible topologies is the square (or just remove the $/2$ part from the formula above).
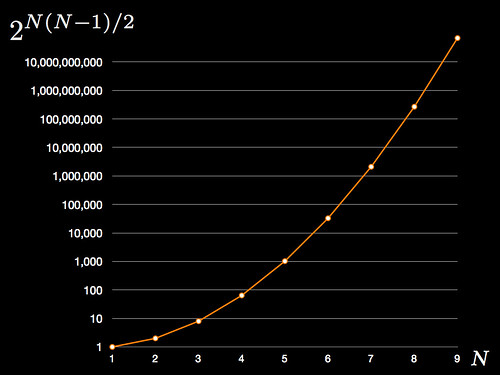
To show how quickly things get out of control, here are some numbers:
$N=1 \Rightarrow 1$ topology
$N=2 \Rightarrow 2$ topologies
$N=3 \Rightarrow 8$ topologies
$N=4 \Rightarrow 64$ topologies
$N=5 \Rightarrow 1024$ topologies
$N=6 \Rightarrow 32,768$ topologies
$N=7 \Rightarrow 2,097,152$ topologies
$N=8 \Rightarrow 268,435,456$ topologies
$N=9 \Rightarrow 68,719,476,736$ topologies
$N=10 \Rightarrow 35,184,372,088,832$ topologies
$N=20 \Rightarrow 1.5693 \times 10^{57}$ topologies
$N=30 \Rightarrow 8.8725 \times 10^{130}$ topologies
$N=40 \Rightarrow 6.3591 \times 10^{234}$ topologies
$N=50 \Rightarrow 5.7776 \times 10^{368}$ topologies
This is the reason why any serious analysis of a network requires the use of mathematical modeling and computer processing: our human brains are not equipped to deal with this kind of exploding complexity.
And for the visual learners, here's a graph denoting the pointlessness of trying to grasp network topologies "by hand" (note logarithmic vertical scale):