There are many documented cases of behavior deviating from the normative "rational" prescription of decision sciences and economics. For example, in the book Predictably Irrational, Dan Ariely tells us how he got a large number of Sloan School MBA students to change their choices using an irrelevant alternative.
The Ariely example has two groups of students choose a subscription type for The Economist. The first group was given three options to choose from: (online only, $\$60$); (paper only, $\$120$); or (paper+online, $\$120$). Overwhelmingly they chose the last option. The second group was given two options : (online only, $\$60$) or (paper+online $\$120$). Overwhelmingly they chose the first option.
Since no one chooses the (paper only, $\$120$) option, it should be irrelevant to the choices. However, removing it makes a large number of respondents change their minds. This is what is called a behavioral bias: an actual behavior that deviates from "rational" choice. (Technically these choices violate the Strong Axiom of Revealed Preference.)
(If you're not convinced that the behavior described is irrational, consider the following isomorphic problem: a waiter offers a group of people three desserts: ice cream, chocolate mousse, and fruit salad; most people choose the fruit salad, no one chooses the mousse. Then the waiter apologizes: it turns out there's no mousse. At that point most of the people who had ordered fruit salad switch to ice cream. This behavior is the same -- use some letters to represent options to remove any doubt -- as the one in Ariely's example. And few people would consider the fruit salad to ice-cream switchers rational.)
Ok, so people do, in some cases (perhaps in a majority of cases) behave in "irrational" ways, as described by the decision science and economics models. This is not entirely surprising, as those models are abstractions of idealized behavior and people are concrete physical entities with limitations and -- some argue -- faulty software.
What is really enlightening is how people who know about this feel about the biases.
IGNORE. Many academic economists and others who use economics models try to ignore these biases. Inasmuch as these biases can be more or less important depending on the decision, the persons involved, and the context, this ignorance might work for the economists, for a while. However, pretending that reality is not real is not a good foundation for Science, or even life.
ATTACK. A number of people use the existence of biases as an attack on established economics. This is how science evolves, with theories being challenged by evidence and eventually changing to incorporate the new phenomena. Some people, however, may be motivated by personal animosity towards economics and decision sciences; this creates a bad environment for knowledge evolution -- it becomes a political game, never good news for Science.
EXPLOIT. Books like Nudge make this explicit, but many people think of these biases as a way to manipulate others' behavior. Manipulate is the appropriate verb here, since these people (maybe with what they think is the best of intentions -- I understand these pave the way to someplace...) want to change others' behavior without actually telling these others what they are doing. In addition to the underhandedness that, were this a commercial application, the Nudgers would be trying to outlaw, this type of attitude reeks of "I know better than others, but they are too stupid to agree." Underhanded manipulation presented as a virtue; the world certainly has changed a lot.
ADDRESS AND MANAGE. A more productive attitude is to design decisions and information systems to minimize the effect of these biases. For example, in the decision above, both scenarios could be presented, the inconsistency pointed out, and then a separate part-worth decision could be addressed (i.e. what are each of the two elements -- print and online -- worth separately?). Note that this is the one attitude that treats behavioral biases as damage and finds way to route decisions around them, unlike the other three attitudes.
In case it's not obvious, my attitude towards these biases is to address and manage them.
Non-work posts by Jose Camoes Silva; repurposed in May 2019 as a blog mostly about innumeracy and related matters, though not exclusively.
Wednesday, September 28, 2011
Sunday, September 18, 2011
Probability interlude: from discrete events to continuous time
Lunchtime fun: the relationship between Bernoulli and Exponential distributions.
Let's say the probability of Joe getting a coupon for Pepsi in any given time interval $\Delta t$, say a month, is given by $p$. This probability depends on a number of things, such as intensity of couponing activity, quality of targeting, Joe not throwing away all junk mail, etc.
For a given integer number of months, $n$, we can easily compute the probability, $P$, of Joe getting at least one coupon during the period, which we'll call $t$, as
$P(n) = 1 - (1-p)^n$.
Since the period $t$ is $t= n \times \Delta t$, we can write that as
$P(t) = 1 - (1-p)^{\frac{t}{\Delta t}}.$
Or, with a bunch of assumptions that we'll assume away,
$P(t) = 1- \exp\left(t \times \frac{\log (1-p)}{\Delta t}\right).$
Note that $\log (1-p)<0$. Defining $r = - \log (1-p) /\Delta t$, we get
$P(t) = 1 - \exp (- r t)$.
And that is the relationship between the Bernoulli distribution and the Exponential distribution.
We can now build continuous-time analyses of couponing activity. Continuous analysis is much easier to do than discrete analysis. Also, though most simulators are, by computational necessity, discrete, building them based on continuous time models is usually simpler and easier to explain to managers using them.
Let's say the probability of Joe getting a coupon for Pepsi in any given time interval $\Delta t$, say a month, is given by $p$. This probability depends on a number of things, such as intensity of couponing activity, quality of targeting, Joe not throwing away all junk mail, etc.
For a given integer number of months, $n$, we can easily compute the probability, $P$, of Joe getting at least one coupon during the period, which we'll call $t$, as
$P(n) = 1 - (1-p)^n$.
Since the period $t$ is $t= n \times \Delta t$, we can write that as
$P(t) = 1 - (1-p)^{\frac{t}{\Delta t}}.$
Or, with a bunch of assumptions that we'll assume away,
$P(t) = 1- \exp\left(t \times \frac{\log (1-p)}{\Delta t}\right).$
Note that $\log (1-p)<0$. Defining $r = - \log (1-p) /\Delta t$, we get
$P(t) = 1 - \exp (- r t)$.
And that is the relationship between the Bernoulli distribution and the Exponential distribution.
We can now build continuous-time analyses of couponing activity. Continuous analysis is much easier to do than discrete analysis. Also, though most simulators are, by computational necessity, discrete, building them based on continuous time models is usually simpler and easier to explain to managers using them.
Labels:
mathematics,
Probability
Saturday, September 17, 2011
Small probabilities, big trouble.
After a long – work-related – hiatus, I'm back to blogging with a downer: the troublesome nature of small probability estimation.
The idea for this post came from a speech by Nassim Nicholas Taleb at Penn. Though the video is a bit rambling, it contains several important points. One that is particularly interesting to me is the difficulty of estimating the probability of rare events.
For illustration, let's consider a Normally distributed random variable $P$, and see what happens when small model errors are introduced. In particular we want to how the probability density $f_{P}(\cdot)$ predicted by four different models changes as a function of distance to zero, $x$. The higher the $x$ the more infrequently the event $P = x$ happens.
The densities are computed in the following table (click for larger):
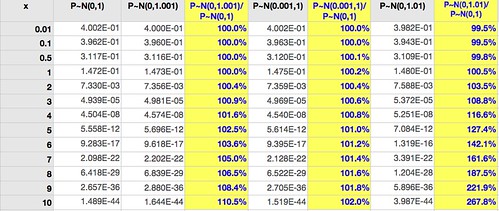
The first column gives $f_{P}(x)$ for $P \sim \mathcal{N}(0,1)$, the base case. The next column is similar except that there's a 0.1% increase in the variance (10 basis points*). The third column is the ratio of these densities. (These are not probabilities, since $P$ is a continuous variable.)
Two observations jump at us:
1. Near the mean, where most events happen, it's very difficult to separate the two cases: the ratio of the densities up to two standard deviations ($x=2$) is very close to 1.
2. Away from the mean, where events are infrequent (but potentially with high impact), the small error of 10 basis points is multiplied: at highly infrequent events ($x>7$) the density is off by over 500 basis points.
So: it's very difficult to tell the models apart with most data, but they make very different predictions for uncommon events. If these events are important when they happen, say a stock market crash, this means trouble.
Moving on, the fourth column uses $P \sim \mathcal{N}(0.001,1)$, the same 10 basis points error, but in the mean rather than the variance. Column five is the ratio of these densities to the base case.
Comparing column five with column three we see that similarly sized errors in mean estimation have less impact than errors in variance estimation. Unfortunately variance is harder to estimate accurately than the mean (it uses the mean estimate as an input, for one), so this only tells us that problems are likely to happen where they are more damaging to model predictive abilities.
Column six shows the effect of a larger variance (100 basis points off the standard, instead of 10); column seven shows the ratio of this density to the base case.
With an error of 1% in the estimate of the variance it's still hard to separate the models within two standard deviations (for a Normal distribution about 95% of all events fall within two standard deviations of the mean), but the error in density estimates at $x=7$ is 62%.
Small probability events are very hard to predict because most of the times all the information available is not enough to choose between models that have very close parameters but these models predict very different things for infrequent cases.
Told you it was a downer.
-- -- --
* Some time ago I read a criticism of this nomenclature by someone who couldn't see its purpose. The purpose is good communication design: when there's a lot of 0.01% and 0.1% being spoken in a noisy environment it's a good idea to say "one basis point" or "ten basis points" instead of "point zero one" or "zero point zero one" or "point zero zero one." It's the same reason we say "Foxtrot Universe Bravo Alpha Romeo" instead of "eff u bee a arr" in audio communication.
NOTE for probabilists appalled at my use of $P$ in $f_{P}(x)$ instead of more traditional nomenclature $f_{X}(x)$ where the uppercase $X$ would mean the variable and the lowercase $x$ the value: most people get confused when they see something like $p=\Pr(x=X)$.
The idea for this post came from a speech by Nassim Nicholas Taleb at Penn. Though the video is a bit rambling, it contains several important points. One that is particularly interesting to me is the difficulty of estimating the probability of rare events.
For illustration, let's consider a Normally distributed random variable $P$, and see what happens when small model errors are introduced. In particular we want to how the probability density $f_{P}(\cdot)$ predicted by four different models changes as a function of distance to zero, $x$. The higher the $x$ the more infrequently the event $P = x$ happens.
The densities are computed in the following table (click for larger):

The first column gives $f_{P}(x)$ for $P \sim \mathcal{N}(0,1)$, the base case. The next column is similar except that there's a 0.1% increase in the variance (10 basis points*). The third column is the ratio of these densities. (These are not probabilities, since $P$ is a continuous variable.)
Two observations jump at us:
1. Near the mean, where most events happen, it's very difficult to separate the two cases: the ratio of the densities up to two standard deviations ($x=2$) is very close to 1.
2. Away from the mean, where events are infrequent (but potentially with high impact), the small error of 10 basis points is multiplied: at highly infrequent events ($x>7$) the density is off by over 500 basis points.
So: it's very difficult to tell the models apart with most data, but they make very different predictions for uncommon events. If these events are important when they happen, say a stock market crash, this means trouble.
Moving on, the fourth column uses $P \sim \mathcal{N}(0.001,1)$, the same 10 basis points error, but in the mean rather than the variance. Column five is the ratio of these densities to the base case.
Comparing column five with column three we see that similarly sized errors in mean estimation have less impact than errors in variance estimation. Unfortunately variance is harder to estimate accurately than the mean (it uses the mean estimate as an input, for one), so this only tells us that problems are likely to happen where they are more damaging to model predictive abilities.
Column six shows the effect of a larger variance (100 basis points off the standard, instead of 10); column seven shows the ratio of this density to the base case.
With an error of 1% in the estimate of the variance it's still hard to separate the models within two standard deviations (for a Normal distribution about 95% of all events fall within two standard deviations of the mean), but the error in density estimates at $x=7$ is 62%.
Small probability events are very hard to predict because most of the times all the information available is not enough to choose between models that have very close parameters but these models predict very different things for infrequent cases.
Told you it was a downer.
-- -- --
* Some time ago I read a criticism of this nomenclature by someone who couldn't see its purpose. The purpose is good communication design: when there's a lot of 0.01% and 0.1% being spoken in a noisy environment it's a good idea to say "one basis point" or "ten basis points" instead of "point zero one" or "zero point zero one" or "point zero zero one." It's the same reason we say "Foxtrot Universe Bravo Alpha Romeo" instead of "eff u bee a arr" in audio communication.
NOTE for probabilists appalled at my use of $P$ in $f_{P}(x)$ instead of more traditional nomenclature $f_{X}(x)$ where the uppercase $X$ would mean the variable and the lowercase $x$ the value: most people get confused when they see something like $p=\Pr(x=X)$.
Subscribe to:
Comments (Atom)